クロスバリデーション(交差検証)の基礎と実践:モデル性能を高める評価手法を徹底解説
機械学習モデルの性能を正確に評価するためには、訓練データとテストデータの分け方が非常に重要になります。もし一度きりの分割で評価を行った場合、その分割の仕方に依存して結果が大きく変動する可能性があります。このような偏りを防ぎ、より客観的で信頼性の高い評価を行うために開発されたのが「クロスバリデーション(交差検証)」です。
クロスバリデーションは、データ全体を複数のサブセットに分け、異なる部分を繰り返し検証用として使用することで、データの偏りを抑えつつ汎化性能を測定します。すべてのデータを訓練とテストの両方に使うため、データ量が限られている場合でも効果的に評価を行うことができます。
本記事では、クロスバリデーションの基本概念を出発点として、ホールドアウト法との違い、代表的な手法の種類、実行の流れ、さらに実務での活用ポイントまでを体系的に解説します。
1. クロスバリデーションとは?
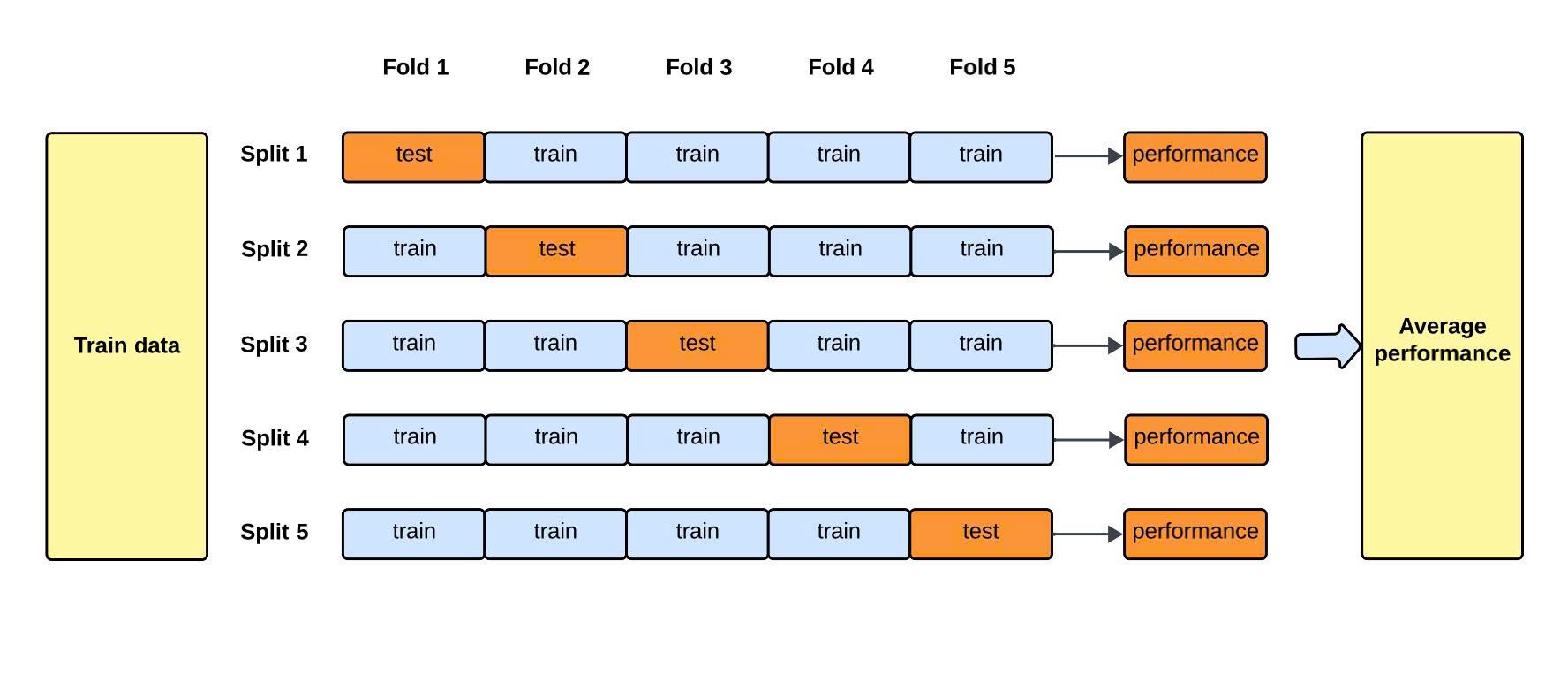
クロスバリデーション(Cross-Validation)は、機械学習モデルの汎化性能を測定するための代表的な評価手法です。データを複数の部分に分割し、それぞれを訓練用と検証用に交互に利用することで、モデルの安定性をより正確に把握できます。特定のデータに依存することなく、モデルが未知のデータにも適切に対応できるかを判断するのに有効です。
この手法では、各分割の評価結果を平均化することで、偶然的なばらつきを減らし、より信頼性の高い性能指標を得られます。特にデータ量が少ない場合や、訓練データとテストデータの分布が完全に一致していない場合でも、クロスバリデーションを用いることでより現実的な評価を実現できます。
また、単なる性能測定だけでなく、ハイパーパラメータ調整やモデル選択にも広く活用されており、実務や研究の場で不可欠な技術といえます。
2. クロスバリデーションとホールドアウト法の違い
クロスバリデーションを理解するうえで、最初に比較されるのが「ホールドアウト法」です。ホールドアウト法は、データセットを一度だけ訓練用とテスト用に分割し、その結果でモデルを評価するという単純な方法です。しかし、この方法では分割の仕方に強く依存し、特定のサンプル構成によっては評価結果が大きく異なることがあります。
一方、クロスバリデーションはデータを複数に分け、各部分を順番に検証データとして使用するため、より安定した評価が得られます。複数回の学習と評価を繰り返すことで、結果の平均がモデルの実際の性能をより正確に反映します。そのため、評価のばらつきを抑えたい場合や限られたデータを最大限に活用したい場合に特に有効です。
次の表は、両者の主な違いを項目別に整理したものです。
項目 | クロスバリデーション | ホールドアウト法 |
| データの使用方法 | データを複数に分割し、全データを訓練・評価に利用 | データを1回だけ訓練・テストに分割 |
| 精度の安定性 | 高い。複数回の平均によりばらつきを抑制 | 低い。分割次第で結果が変動 |
| データ効率 | 高い | 低い |
| 計算コスト | 高い(繰り返し学習が必要) | 低い(1回の学習で完了) |
ホールドアウト法はシンプルで計算量も少ないため、モデルの初期検証などには適しています。しかし、実際に性能を比較・評価する場面では、クロスバリデーションの方が信頼性の高い結果を得ることができます。
3. クロスバリデーションの種類
クロスバリデーションにはさまざまな手法が存在し、データの性質やタスクの目的によって最適な方法を選択することが求められます。たとえば、データ量が多い場合は計算コストを考慮したk分割法、小規模データの場合は精密な評価を可能にするLOOCV(Leave-One-Out Cross-Validation)、クラス不均衡がある場合は層化分割法などが代表的です。
各手法には長所と短所があり、それぞれの特性を理解することで、より適切な評価設計が可能になります。以下では、代表的な3つのクロスバリデーション手法について詳しく見ていきます。
手法名 | 特徴 | 利点 | 注意点 |
| k分割交差検証 | データをk分割して評価を繰り返す基本手法 | 評価の安定性と効率のバランスが良い | kの設定により計算コストが変化 |
| LOOCV | 1サンプルを除いて繰り返し検証 | 高精度評価が可能 | 計算量が非常に多い |
| 層化k分割交差検証 | クラス比を維持して分割 | 不均衡データに適応可能 | 分類タスク以外では非対応の場合あり |
3.1 k分割交差検証(k-Fold Cross-Validation)
k分割交差検証は、最も広く利用されているクロスバリデーション手法です。データセットをk個の等しい部分に分け、各部分を一度ずつテストデータとして利用します。これにより、すべてのデータが一度はテストに使用され、残りのk−1部分を訓練データとして用いることになります。最終的に、k回の評価結果を平均してモデルの汎化性能を算出します。
この方法の強みは、データの使用効率が高く、結果のばらつきを抑制できる点にあります。kの値を増やすほど精密な評価が可能になりますが、その分計算時間が増加します。一般的に、5分割または10分割が標準的な設定としてよく用いられます。
3.2 Leave-One-Out Cross-Validation(LOOCV)
LOOCVは、k分割交差検証の特殊なケースで、分割数kをデータ数と同じに設定する方法です。つまり、1つのサンプルをテストデータ、残りのすべてを訓練データとして用い、これを全サンプルについて繰り返します。
この手法は理論的に非常に厳密であり、限られたデータを最大限に活用できます。ただし、データ量が多い場合には、訓練・評価を繰り返す回数が膨大となり、実行時間が長くなる点に注意が必要です。少量データセットにおけるモデル比較やアルゴリズム検証には適しています。
3.3 層化k分割交差検証(Stratified k-Fold Cross-Validation)
層化k分割交差検証は、分類問題でしばしば用いられる手法で、各分割内でクラスの分布をできる限り均等に保つようにデータを分割します。これにより、クラス不均衡のあるデータセットでも、公平な評価を行うことができます。
特に、ラベルごとのサンプル数に偏りがある場合には、通常のk分割交差検証よりも適切な結果を得られます。層化処理を行うことで、モデルが少数クラスを過小評価するリスクを軽減し、より現実的な性能評価が可能となります。
これらの違いを正確に理解し、データ構造やタスク特性に応じて適切な手法を選択することが、信頼できるモデル評価の第一歩となります。
4. クロスバリデーションの実行
クロスバリデーションを実施する際には、まずデータをランダムにシャッフルして順序の偏りを取り除くことが重要です。その後、選択した分割法に基づいてデータを訓練用と検証用に分け、モデルの学習と評価を繰り返します。
実装の際には、Pythonの機械学習ライブラリ「scikit-learn」に含まれるKFold、StratifiedKFold、LeaveOneOutなどのクラスを使用することで、手作業による分割を避け、効率的に処理を行うことができます。
また、クロスバリデーションの結果として得られる複数のスコアを平均し、分散を確認することで、モデルの安定性をより詳細に把握することが可能です。異なるアルゴリズムやハイパーパラメータを比較する際にも、クロスバリデーションを組み合わせることで、より公平で客観的な評価を行えます。
5. クロスバリデーションの活用ポイント
クロスバリデーションは、単なる評価手法にとどまらず、実務的な機械学習プロセスにおける重要な判断材料として活用されます。ここでは、代表的な3つの応用例を紹介します。

5.1 モデル選択への活用
複数のアルゴリズムやモデル構造を比較する際、クロスバリデーションを利用することで、どのモデルが最も安定した性能を発揮するかを客観的に評価できます。単一のテストデータによる比較よりも信頼性が高く、過剰評価のリスクを抑えることができます。
5.2 ハイパーパラメータ調整への活用
ハイパーパラメータの最適化においても、クロスバリデーションは欠かせません。グリッドサーチやランダムサーチなどの探索手法と組み合わせることで、複数の設定を一貫した条件下で比較でき、過学習を防ぎながら最適な構成を導き出せます。
5.3 モデル安定性の検証
クロスバリデーションの結果を分析することで、モデルの安定性を確認できます。例えば、各分割におけるスコアの分散を調べることで、モデルが特定のデータに依存していないかを判断でき、実運用での信頼性を高める助けとなります。
おわりに
クロスバリデーションは、機械学習モデルの性能を正確かつ客観的に評価するための不可欠な手法です。限られたデータを最大限に活用でき、過学習を防ぎながらモデルの真の汎化能力を測定できます。
k分割交差検証、LOOCV、層化k分割交差検証などの各手法にはそれぞれ特徴があり、データ規模や目的に応じて適切に選択することが重要です。これらを理解し正しく運用することで、より信頼性の高いモデル開発が可能になります。
さらに、クロスバリデーションはモデル選択・パラメータ調整・安定性検証など、実務的な応用範囲が広く、AI開発における評価基盤として極めて重要な位置を占めています。堅牢なモデル構築を目指す上で、クロスバリデーションの理解と実践は欠かせません。


 EN
EN JP
JP KR
KR











