バッチ正規化（Batch Normalization）の仕組みと効果を徹底解説

深層学習（Deep Learning）の発展に伴い、ネットワークの層数が増加し、モデルの表現力が飛躍的に向上しました。しかしその一方で、「勾配消失」や「学習不安定化」といった課題が顕在化しました。これらの問題を効果的に緩和し、学習を安定化させる技術として登場したのがバッチ正規化（Batch Normalization, BN）です。

バッチ正規化は、各層に入力されるデータの分布を整えることで、ネットワーク全体の学習を滑らかにし、収束を早める役割を果たします。現在では、CNN（畳み込みニューラルネットワーク）やTransformerなど、ほとんどの深層モデルで標準的に導入される技術となっています。

本記事では、バッチ正規化の仕組みを数学的・概念的に整理し、その導入効果や注意点、他の正規化手法との違いを体系的に解説します。 

1. バッチ正規化とは？ 

バッチ正規化とは、ニューラルネットワークの学習を安定化させ、効率を高めるための手法です。学習中、各層の入力データ（特徴量）の分布が変化してしまう現象を「内部共変量シフト（Internal Covariate Shift）」と呼びますが、バッチ正規化はこれを抑える役割を果たします。 

具体的には、ミニバッチごとに各特徴量の平均と分散を計算し、データを平均0・分散1になるように正規化します。その後、スケーリング（γ）とシフト（β）のパラメータを導入して、ネットワークが柔軟に最適な分布を再学習できるようにします。これにより、勾配消失のリスクが減少し、学習速度の向上や過学習の抑制にもつながります。 

バッチ正規化は、深層学習モデルの標準的なテクニックとして、CNNやRNNなど幅広いネットワーク構造で利用されています。 

2. バッチ正規化が導入された背景 

ニューラルネットワークの学習では、各層のパラメータ更新によって入力分布が大きく変動し、後続層がその変化に追随できなくなることがあります。これを内部共変量シフト（Internal Covariate Shift）と呼びます。 

この問題により、学習が遅くなる・勾配が消失または爆発する・学習率調整が困難になるといった現象が発生します。バッチ正規化はこの課題を解消するために提案され、入力分布を一定範囲に保つことで、ネットワーク全体を安定化させます。結果として、より高い学習率でも安定的に訓練が可能となり、収束速度の向上が実現されました。 

3. バッチ正規化の仕組み  

バッチ正規化（Batch Normalization）は、ニューラルネットワークの学習を安定化させ、収束を早めるための重要な手法です。その基本的な考え方は、各レイヤーの出力を正規化し（平均0・分散1に調整）、その後に学習可能なスケールとシフトのパラメータを適用するというものです。この工程によって、層ごとの出力が極端に偏ることを防ぎ、勾配消失や勾配爆発を抑制します。 

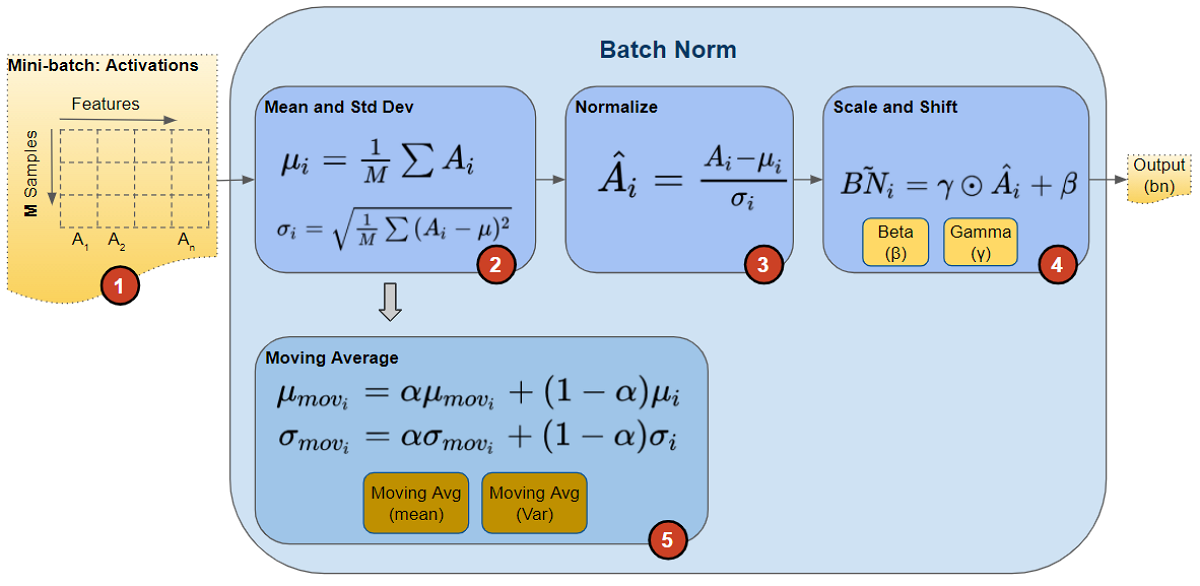
3.1 ミニバッチ単位での計算 

ニューラルネットワークの学習では、すべてのデータを一度に処理するのではなく、ミニバッチと呼ばれる小規模なデータセットに分けて学習を行います。 
バッチ正規化では、このミニバッチごとに以下のような計算が行われます。 

• 各ミニバッチ内の出力値から平均を求める。 
• 同じミニバッチ内で分散を計算する。 

この平均と分散を使って、そのバッチ内の出力分布を標準化します。これにより、ネットワークは異なる入力でも安定した学習を進めることが可能になります。 

3.2 標準化（正規化）の処理 

計算された平均と分散を用いて、各データポイントの値を標準化します。具体的には、各出力から平均を引き、分散の平方根で割ることで、平均0・分散1のスケールに変換します。 

この処理によって、すべてのデータが同じスケールで扱われるようになり、層ごとの値のばらつきが抑えられます。結果として、学習の安定性と効率が大きく向上します。 

3.3 スケールとシフトの調整 

単に標準化しただけでは、ネットワークの表現力が制限されてしまうため、バッチ正規化ではその後に学習可能なパラメータであるスケール（γ）とシフト（β）を導入します。 

• スケール（γ）：標準化後の値を拡大・縮小する係数。 
• シフト（β）：標準化後の値に一定のオフセットを加える項。 

この調整により、ネットワークは単純に正規化するだけでなく、データの分布を学習に合わせて柔軟に変化させることができます。スケールとシフトを学習することで、モデル全体の表現能力を損なわずに安定した学習が実現されます。 

バッチ正規化は単なる正規化手法にとどまらず、「学習の安定化」と「モデルの表現力維持」という2つの効果を両立させる重要な技術として、ディープラーニングの発展に大きく貢献しています。 

4. バッチ正規化のバリエーション  

正規化は、ニューラルネットワークの学習を安定化させるために欠かせない技術です。代表的なBatch Normalization（BN）のほかにも、データ構造やモデル特性に応じてさまざまな正規化手法が提案されています。以下では、それぞれの特徴と適用分野を解説します。 

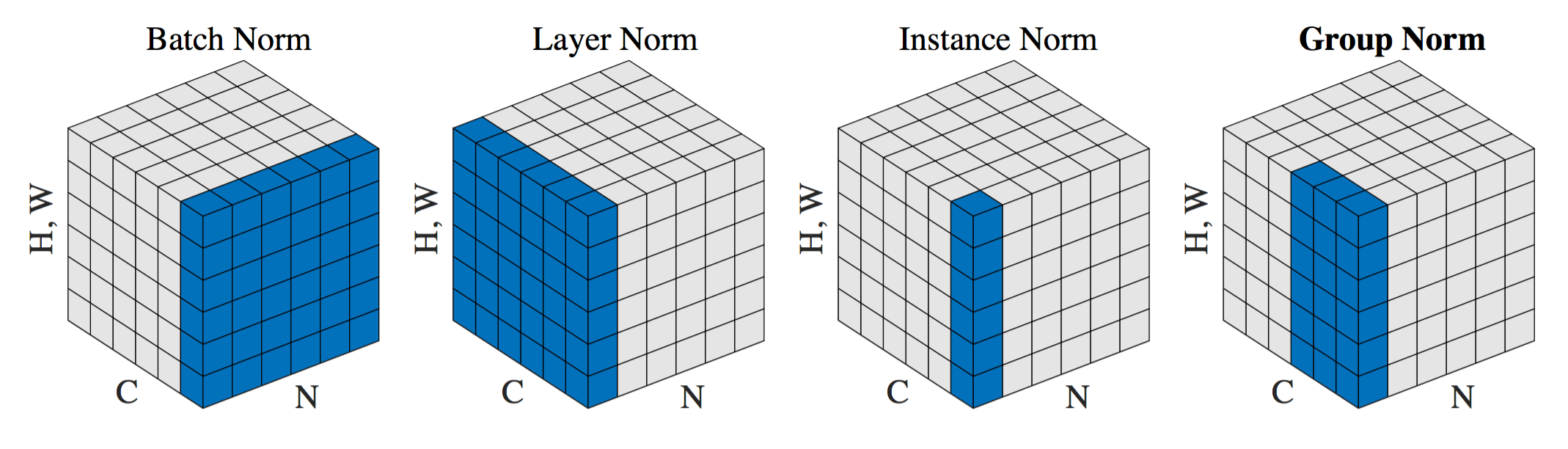
4.1 Layer Normalization（レイヤー正規化） 

Layer Normalizationは、各サンプルの層全体を対象に正規化を行う手法です。バッチ単位ではなく、1サンプルごとの特徴量方向で平均と分散を計算します。 

そのため、バッチサイズに依存せず、逐次処理モデル（RNNやTransformerなど）で高い安定性を発揮します。自然言語処理分野では、この手法が標準的に採用されています。 

4.2 Instance Normalization（インスタンス正規化） 

Instance Normalizationは、各チャンネルごとに正規化を行う手法です。入力画像1枚に対してチャネル単位でスケーリング・シフトを適用します。 

この特性から、スタイル変換（Style Transfer）や画像生成タスクなど、画像の見た目や質感を制御する分野で活用されています。特にGAN系の生成モデルでは、生成結果の一貫性や質感表現を改善するためによく用いられます。 

4.3 Group Normalization（グループ正規化） 

Group Normalizationは、チャンネルをいくつかのグループに分け、グループ単位で正規化を行う手法です。BNのようにバッチサイズに依存せず、小規模データセットでも安定した性能を発揮します。 

特に、GPUメモリの制約でミニバッチが小さくなる場合や、医療画像のような少数データ学習において有効です。CNN系モデルでBNの代替として利用されることが多く、柔軟性の高い正規化手法といえます。 

手法選択のポイント 

バッチ正規化は大規模バッチ学習に最適ですが、バッチサイズが極端に小さい場合や逐次処理を伴うモデルでは性能が低下することがあります。そのため、モデル構造やタスク特性に応じて、レイヤー正規化・インスタンス正規化・グループ正規化などの手法を適切に選択することが重要です。 

実際の運用では、TransformerにはLayer Normalization、GANにはInstance Normalization、医療や小規模学習にはGroup Normalizationが採用されるケースが多く見られます。 

5. バッチ正規化の効果 

バッチ正規化（Batch Normalization, BN）は、ニューラルネットワークの学習過程を安定化し、精度と効率を大きく改善するための代表的な手法です。以下では、BNがもたらす主要な効果を詳しく見ていきます。 

5.1 学習の安定化 

バッチ正規化は、各層の出力を正規化することで勾配のスケールを一定に保ち、学習の不安定化を防ぎます。これにより、勾配爆発や発散といった問題が発生しにくくなります。 

特に深いネットワークでは、勾配が層を伝わる過程で極端に大きくなったり小さくなったりすることがありますが、バッチ正規化の導入によりその変動が抑えられ、より滑らかな学習が可能となります。 

5.2 収束の高速化 

バッチ正規化は、各層の出力分布を安定化させるため、より高い学習率（learning rate）を安全に設定することができます。その結果、収束までのエポック数が減り、学習が効率化します。 

また、初期段階から勾配の伝播が適切に保たれるため、ハイパーパラメータの微調整に費やす時間も短縮できます。これが、バッチ正規化が実務的にも重宝される理由の一つです。 

5.3 過学習の抑制 

バッチ正規化は、バッチ単位で異なる統計量を用いるため、出力にわずかなランダム性が加わります。この性質がノイズとして働き、軽度の正則化（regularization）効果を生み出します。 

この効果により、モデルが訓練データに過剰適合することを防ぎ、汎化性能（generalization）を自然に高める傾向があります。 

5.4 初期値への依存低減 

バッチ正規化を導入することで、パラメータ初期化の影響を受けにくくなります。これは、ネットワークの各層が一定の分布を保ったまま学習を進められるためです。 

その結果、初期化戦略に過度に依存せずとも、安定した精度を得やすくなり、モデル設計が容易になります。 

5.5 内部共変量シフトの軽減 

バッチ正規化の基本的な目的は、内部共変量シフト（Internal Covariate Shift） —すなわち、層ごとに入力分布が変化して学習が不安定になる現象—を緩和することです。 

各層の出力を正規化することで、後続層が常に一定の分布を前提に学習できるようになり、ネットワーク全体の訓練がスムーズになります。 

5.6 勾配消失の緩和 

深層ネットワークでは、活性化関数（特にsigmoidやtanh）を通す際に勾配が小さくなり、学習が進まない「勾配消失問題」が発生しやすい傾向にあります。バッチ正規化は、出力を正規化することで活性化関数の入力分布を適度に保ち、この問題を軽減します。 

これにより、より深いモデルでも安定した学習が可能となり、ResNetやTransformerなどの大規模アーキテクチャの基盤を支える技術として活用されています。 

5.7 汎化性能の向上 

バッチ正規化によって学習過程が安定し、ノイズ的効果が加わることで、未知データに対する汎化性能が向上します。実際、多くの研究でバッチ正規化を導入したモデルがテストデータにおいても高い精度を示しています。 

この特性は、バッチ正規化が単なる「学習の補助」ではなく、モデル全体の性能を底上げする要素技術として機能していることを意味します。 

 
バッチ正規化は、学習の安定化・高速化・汎化性能向上など、多面的な恩恵をもたらす正規化手法です。これらの効果により、バッチ正規化は現在の深層学習モデルにおいてほぼ標準的な構成要素となっています。 

6. バッチ正規化の課題と注意点 

バッチ正規化（Batch Normalization, BN）は、ディープラーニングの学習を安定化し、収束を加速させる重要な手法として広く用いられています。しかし、その有効性の裏には、いくつかの制約や課題も存在します。以下に主な注意点を整理します。 

6.1 バッチサイズ依存性 

BNはバッチ単位で統計量（平均・分散）を計算するため、バッチサイズが小さいと統計が不安定になり、出力がばらつきやすくなります。特にGPUメモリ制約や少量データ学習では、モデルの収束が遅れたり精度が低下することがあります。 

この問題に対しては、Layer Normalization（LN） や Group Normalization（GN） のようにバッチに依存しない手法を用いることで、安定した学習を実現できます。 

6.2 推論時の統計差異 

学習時にはミニバッチごとの統計値を使用しますが、推論時には学習過程で蓄積された移動平均値を利用します。この差により、訓練時と実環境でデータ分布が異なる場合、モデル出力にずれが生じる可能性があります。 

この問題を回避するためには、推論前に統計量を再計算（リキャリブレーション） するか、分布変動の少ない特徴量設計を行うことが有効です。 

6.3 計算コストの増加 

BNは各バッチで平均・分散を求めるため、追加の演算処理が必要になります。特に大規模なCNNや高解像度画像を扱う場合、処理時間やメモリ使用量の増加が無視できません。 

処理効率を重視する場合は、推論時にBNを統合（folding） したり、軽量な正規化手法（例：Weight Standardization） を導入することで、負荷を軽減できます。 

6.4 分散環境での同期問題 

複数GPUを用いる分散学習では、各デバイスで独立した統計量が計算されるため、バッチ全体での整合性が崩れることがあります。この不一致は学習の不安定化を招く要因になります。 

この対策として、各GPU間で統計情報を共有する SyncBatchNorm が用いられます。ただし、通信オーバーヘッドが増大するため、環境に応じたバランス設計が求められます。 

6.5 内部共変量シフトの残存問題 

BNの導入目的の一つは「内部共変量シフト（Internal Covariate Shift）」の抑制ですが、後続の研究では、BNがこの問題を完全には解消していないことが指摘されています。BNは勾配伝播を安定化させる効果を持つ一方で、分布変化そのものを根本的に防ぐわけではありません。 

つまり、BNは「分布の変化を軽減する」よりも「勾配を扱いやすくする」効果が主であると再解釈されています。この点を理解した上で、アーキテクチャ設計時に他の正規化手法との併用を検討することが重要です。 

6.6 RNNへの適用の難しさ 

BNは主にCNNやTransformerのような並列処理構造のモデルで効果を発揮しますが、RNN（再帰型ニューラルネットワーク） には適用が難しいとされています。これは、RNNが時系列方向に内部状態を保持するため、バッチ単位での統計計算が一貫しないからです。 

このため、RNNではBNの代わりに Layer Normalization や Weight Normalization がよく用いられます。これらの手法は時系列構造を保ちながら安定化を図るため、音声認識や自然言語処理の分野でより効果的です。 

BNは深層学習の安定化に不可欠な技術である一方、万能ではありません。モデル構造、バッチサイズ、実行環境に応じて、正規化手法を柔軟に選択・組み合わせることが、高精度かつ効率的な学習を実現する鍵となります。 

おわりに 

バッチ正規化（Batch Normalization）は、深層学習の安定性と効率を飛躍的に高めた革新的な技術です。学習過程で各層の入力データを正規化し、内部のデータ分布の偏りを抑えることで、学習を安定させ、勾配消失などの問題を軽減します。その結果、より高い精度と高速な収束を実現できるため、現在では多くのAIモデルで標準的に採用されています。 

しかし、バッチ正規化はすべてのケースにおいて万能というわけではありません。特にバッチサイズが小さい場合や、時系列・生成モデルなどデータの特性が異なるタスクでは、期待する効果が得られにくいこともあります。そうした状況では、Layer NormalizationやGroup Normalizationといった代替手法の利用が検討されます。 

重要なのは、バッチ正規化の原理と役割を正しく理解し、モデルの構造やデータ特性に合わせて適切に組み込むことです。これが、AI開発における性能最適化の第一歩となるでしょう。